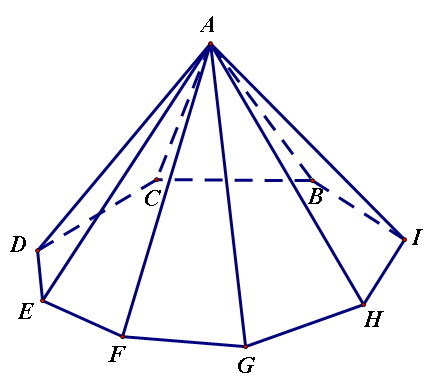
八棱锥图片

怎样画八棱锥?素描
图片尺寸434x389
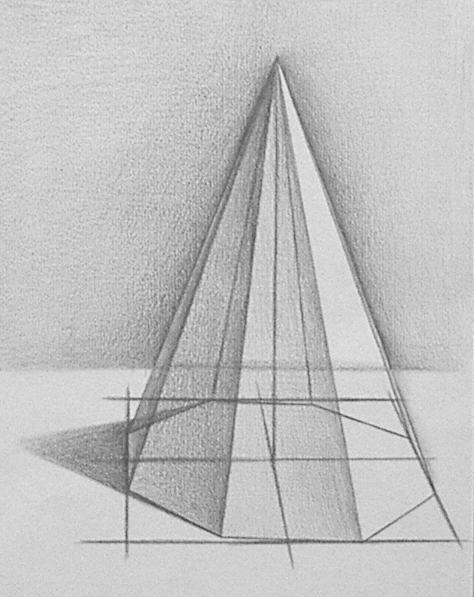
怎样画八棱锥?素描
图片尺寸474x597
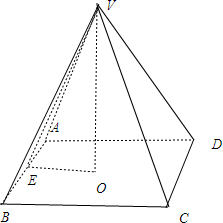
正八面体是由两个正四棱锥对接而成, 设正四棱锥p-abcd,高po,垂足o,则
图片尺寸914x481
素描基础教程-八棱锥结构-1
图片尺寸1728x1080
【一笔一画打形】八棱锥
图片尺寸1168x1580
由已知得到:底面的中心就是过球心的平面,因此四棱锥的高po就是球的
图片尺寸322x348
已知四棱锥p-abcd的底面abcd是菱形.pa⊥平面abcd.pa=ad=ac.
图片尺寸275x224
(1)求证: ‖ ;(2)求三棱锥 的体积. _百度教育
图片尺寸244x212
(Ⅰ)求棱锥的体积;(Ⅱ)求证:平面平面;(Ⅲ)在线段上是否存在一点,使
图片尺寸239x266
由八个面围成的几何体,每一个面都是正三角形,并且有四个顶点a,b,c,d
图片尺寸165x169
有关正八面体,正四面体的有趣问题_棱锥
图片尺寸673x282
如图,在三棱锥中,,,°,平面平面,,分别为,中点.
图片尺寸235x262
5-8 补全三棱锥被截切后的俯视图并求左视图.
图片尺寸1080x810
正四棱锥的底面边长为2cm,侧面与底面所成二面角的大小为60°,则该四
图片尺寸223x223
面是全等的正三角形,可以利用对称关系,先求出正四棱锥s-abcd的体积
图片尺寸500x400
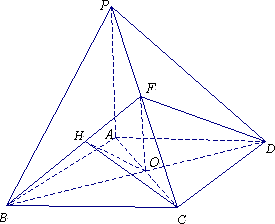
(1)证明:ph ⊥平面abcd ; (2)若ph =1,ad 2,fc =1,求三棱锥e -bcf 的
图片尺寸992x702
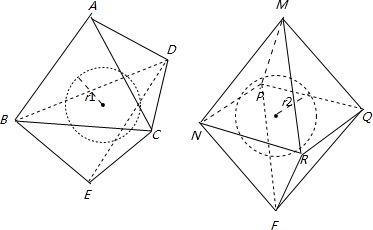
八面体中的正四棱锥m-npqr的高为h2,如图所示再设六面体中的正三棱锥a
图片尺寸373x230
如图,四棱锥p -abcd 中,底面abcd 为矩形,pa ⊥底面abcd
图片尺寸682x783
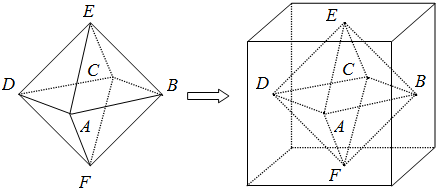
两个相同的正四棱锥底面重合组成一个八面体可放于棱长为1的正方体中
图片尺寸436x188
第九章第八节棱锥的概念和性质ppt下载
图片尺寸800x600