密铺三维空间

40共享分×关 键 词:密集立方体高清图片 背景 立方体 密集 模板 空间
图片尺寸1024x1024
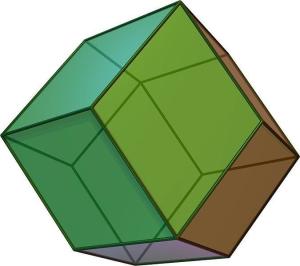
菱形十二面体
图片尺寸686x515
2016最新苏教版五年级下册数学《奇妙的图形密铺》课件3ppt
图片尺寸1080x810
地球上像埃舍尔名画的超现实几何空间
图片尺寸750x913
180.00
图片尺寸887x838
十二面体菱形十二面体展开图菱形十二面体能单独密铺一个无限三维空间
图片尺寸300x266
校园情射
图片尺寸550x324
如何用figma快速绘制空间密铺动画
图片尺寸1080x1440
201811514广东番禺中学附属学校ta的空间关注ta下载该模型所需豌豆:8
图片尺寸800x600
上一期讲了一种空间密铺问题.本期再来讲一种.
图片尺寸630x286
在埃舍尔的艺术生涯中,他还对多面体和多维空间进行了深入的探索和
图片尺寸650x663
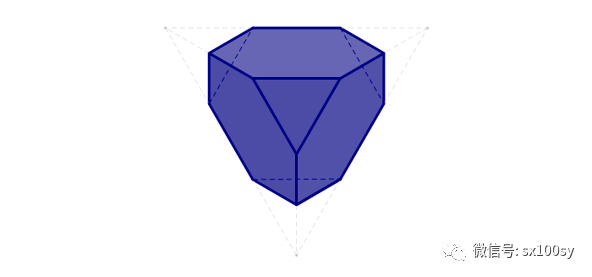
它旨在确定能够完美填充(或者说"密铺")三维空间的多面体
图片尺寸1080x637
有边长相等的正方形和等级边三角形若干,你能用这些
图片尺寸326x338
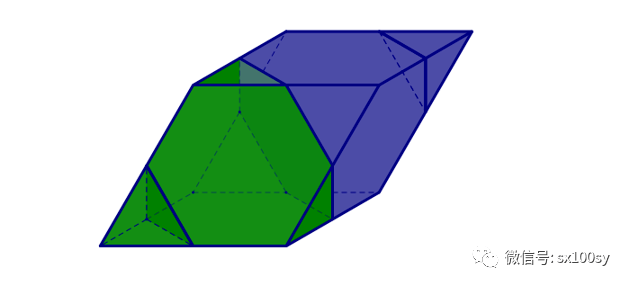
菱形六角化十二面体可以密铺于三维空间密铺在几何学中,菱形六角化
图片尺寸1294x971
在埃舍尔的艺术生涯中,他还对多面体和多维空间进行了深入的探索和
图片尺寸660x557
因为正六面体(正方体)是三维空间中唯一可密铺空间的正多面体.
图片尺寸480x272
上一期讲了一种空间密铺问题.本期再来讲一种.
图片尺寸728x454
美国数学家发现完美镶嵌五边形 可无缝密铺平面(图)
图片尺寸600x357
上一期讲了一种空间密铺问题.本期再来讲一种.
图片尺寸592x277
d{7,3}dt{7,3}j{7,3}k{7,3}o{7,3}m{7,3}g{7,3}例如:三维空间的正方
图片尺寸938x930