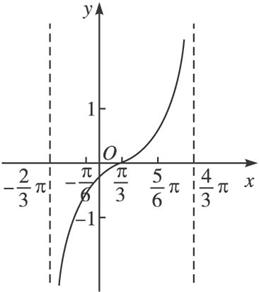
tan(1/x)的图像

y = tan x -3π/2 o 3π/2
图片尺寸1080x810
正切函数tan(x)的图像
图片尺寸640x483p> b>三角函数 /b>是 a target="_blank" href="/item/基本初等函数/
图片尺寸296x269
y =tan x 的性质 (1)定义域是{x |x ≠k π π2
图片尺寸563x333
2y tanx,x r(k z)
图片尺寸1632x603
3正切函数的图像与性质1ppt 函数y tan x (x 正切曲线 3 2 2
图片尺寸1080x810
577_513
图片尺寸577x513
正切函数y=tanx(x≠kπ π/2,k∈z)的函数图像又叫正切曲线.
图片尺寸640x439
下列图形分别是①$y=| an x|$;②$y= an x$;③$y= an left(-x
图片尺寸391x210
描点作线画图: ∞…10-1…-∞)-tan(…0…--…-…-x解:(1)列表:=z)将
图片尺寸259x292
图像如上,性质为在(kπ-π/2,kπ π/2)上递增 但在整个定义域区间内
图片尺寸943x538
y=1/tanx图像怎么画的?在(0,π/2)上单调增吗?
图片尺寸450x353
因此tan(x)是周期为π的周期函数,那么其在整个实数域上的图像为
图片尺寸640x522
href=/item《第15课时 三角函数的图像与性质(1)》求函数ytan2x的定义
图片尺寸443x458
请问arctan1/x的连续性是什么样的?能从间断点说明一下吗?
图片尺寸1070x824
的性质和图像》课件ppt 有效构建课堂 利用正切线画出函数y tan x
图片尺寸1080x810
tanx的反函数
图片尺寸595x395
正切函数y =tan x ,x ∈r ,x
图片尺寸571x379
追问: 能解释下吗 我都看晕了 追答: 图中弯曲的线就是tanx的图像,两
图片尺寸434x227
> 正切函数的图像与性质导学案自主预习探究问题二利用正切线作y tanx
图片尺寸556x267
猜你喜欢:tan1/x的图像cotx图像和tanx图像arctan1/x的图像tanx的图像y=tan|x|的图像y=arctan1/x的图像arctanx的图像sin1/x的图像tan函数的图像cos(1/x)的图像arctanx图像tan图像y=sin|x|的图像tanx图像y=1/x的图像tan图像和性质sincostan图像y等于x的三次方的图像tanx图象e的x分之一的图像arcsinx图像arccotx图像根号x的图像x=y^2的图像y=√x的图像cotx图像arccosx图像y=cos|x|的图像y等于x分之一的图像x的三次方图像盒装牛奶包装材料火影忍者鼬4k超清壁纸邹市明老婆冉莹颖郭富城演唱会2008年带烟酒的丧图片白色羊羔毛外套女内搭江枫渔火对愁眠简笔画金灶电水壶价格洛奇溪堂民宿酒店斗鸡什么腿为上品图片祝您五一节日快乐一根金针菇特写